参考
ダイアトニックコードには似たようなコードを共有する調があります。
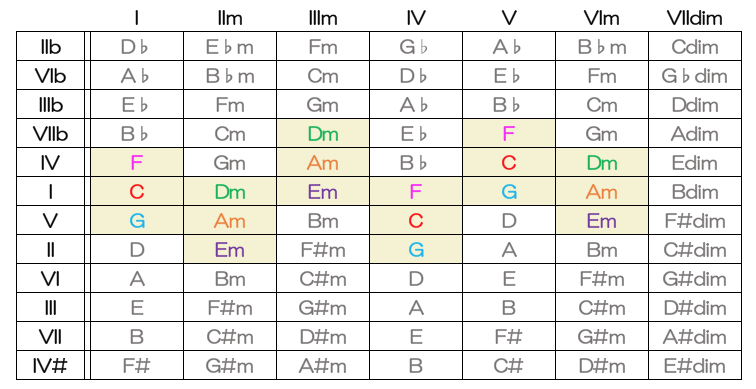
Cメジャーキーのダイアトニックコードと共通したコードネームを持つキーが
Gメジャーキー;3つ共通(属調)
Fメジャーキー;3つ共通(下属調)
Dメジャーキー;2つ共通
Bbメジャーキー;2つ共通
これらの共通したコードをピヴォットコード=pivot chord(蝶番コード)と呼ぶ、と私は学びました。ドアと壁をつなげて可動させる軸の部分のことを蝶番(ちょうつがい)と呼ぶ、ということからきています。
すごく古そうな発想ですがなかなかオツです。
2つの調を接合させる共通コードですね。
現代的感覚で言うとしたら「インターフェース」「HUB」「ジャンクション」みたいなかんじで二つの機器を接続する装置とかをイメージいただければ良いと思います。
楽曲の流れの中でこれらの共通コードを使うことで、巧みにスムーズに転調することができる、とされたコードです。でも意外と使う人のセンスだった、というのが現実ですが。
C |Dm |Em |Dm Cm|Bb |
などとpivotを挟んでCメジャーキーからBフラットメジャーキーに移行したりします。
最近はpivotを使わない突然転調の方が主流です。
こんな概念ちまちま使うよりもDAWや機械の勢いに任せてガラッと変えてみたら一層劇的だった、と我々は気がついたからです。
シンセキーボードなら、トランスポーズボタンを押せば劇的な転調!!(笑)
そういう思考が不定調性論的思考です。起こった出来事の印象がいい感じならそれを用いる。
当ブログではユーミン楽曲が巧みにpivotを使い、ユーミンカラー=淡いグラデーションを作っています。さすがです。こっちは細かい職人技ですね。
送りバントで自分も1塁とっちゃう、地味だけど、悪いことは何もない匠の技です。
I度調とV度調のグラデーション転調~ユーミン歌詞・コード考43
"恋をしなければ見ることのない ダイアモンドの街角"~ユーミン歌詞・コード考44
..他にももっとあります。
逆に共通のコードがないキーに移行すると音階音も変わるのでガラリと変わった転調感になります。半音上転調とかね。
で、これが四和音だと、ちょと減ります。
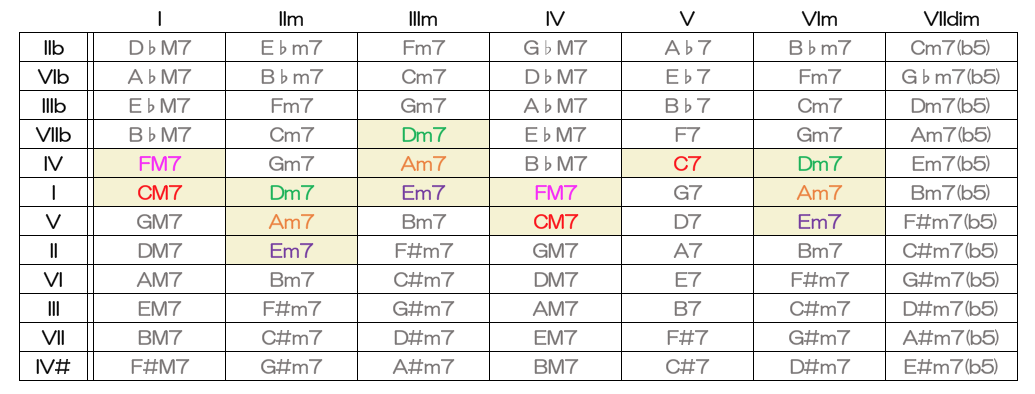
GがG7になるので。
で、これを拡張する方法として、同主調を絡ませる、という発想です。
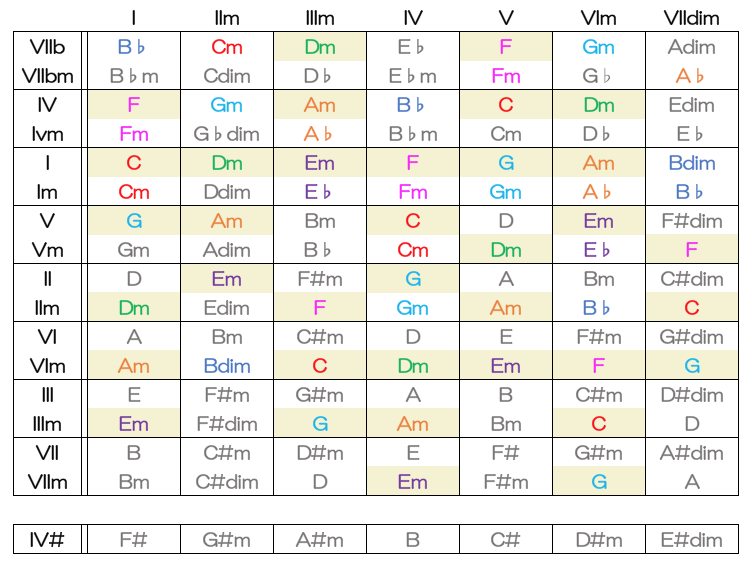
中段にI,Imのところを見てください。
CとCmの二つのキーがグループになっています。
この二つのグループを使うと今っぽい=ビートルズが推し進めたハイブリッドキーの楽曲ができます。
C |F |Bb |Eb |
みたいな。これら四つのコードはC,Cmの中に出てきます。
これらを一つのグループとすれば、上の表のように、かなり広範囲に共通和音が現れます。これも四和音表載せておきます。
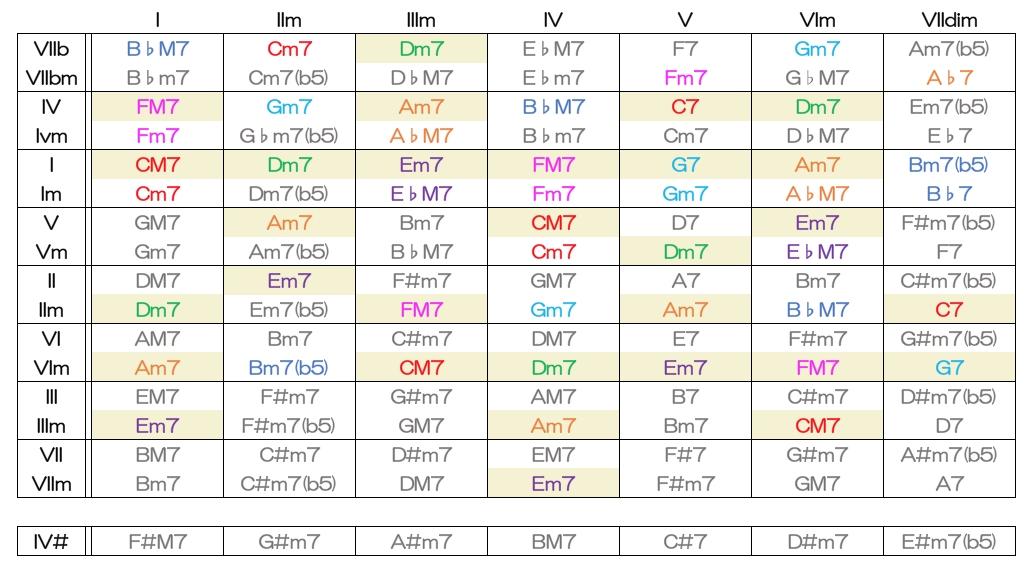
なんでジャズがII-Vを巧みに用いながら転調が展開できたか、ということを考える時、結局V7を用いればどこにでもいけるし、その前置きとなるIIm7はm7タイプのコードで、最も共通性の高いコードであるので、色々置いているうちに戻せる、というのは、こうしたpivot感を活用した伝統に則った技だったんですね。ジャズはすごい。
==余談==
例えば、
CM7|Em7 |Bm7 |C#m7|
G#m7|GM7 |A7 |Dm7G7|
音はこちら
こういった不定調性的な進行は、pivot概念の拡張、と考えることもできます。
あとは考え方やアプローチの違いによって概念の名前が変わってくるのでしょう。
私自身は、キーを考えながらコードを置く、というよりもコードを置いていきながら考えるので、pivotを意識しているわけではありません。
CM7|Em7 |(Cメジャーキー)
Em7 |Bm7 |(Bマイナーキー)
C#m7|G#m7|(Bメジャーキー)
G#m7|(Eメジャーキー)GM7(Eマイナーキー) |Dm7G7|
GM7 |A7(Dメジャーキー)
|Dm7(Dマイナーキー)
|Dm7 |G7 |(Cメジャーキー)
という解釈が可能です。
キー解釈で厳密に色合いをチェックしたい時このような考え方もできます。
こういう風に聞いて考える人と考えない人がいると思います。私は後者です。
不定調性論ではこうしたキー分析をしません。
音楽家の体の中には体得した響きが入っていて、音楽家各位の「連鎖欲求」「連結のクオリア」が起動し始めるからです。本来はそれに委ねて制作したほうが"自分に則った音楽制作"ができます。「ここでpivot使わなきゃ」とは考えず、逆に「最近突然転調も飽きたから、pivot挟んだらどうなるのかな??」という感じで使ってみると意外な響きになって「ぉおおおお!!!」となったりするんです。それが音楽的なクオリアを刺激して制作が捗る、というような感覚が不定調性論的な音楽制作のあり方です。
それが分析できるかどうかは結果論です。
様々な解釈・作成方法があると思いますが、今日は受講生に「表作ってくれない?」と言われて作ったpivotのお話でした。