上方領域
~c-c#-d -d#-e-f- f#- g-g#-a-a#- b- c~
下方領域
~c-b-b♭-a-a♭-g-g♭-f-e- e♭-d-d♭-c~
c:f#すなわち増四度の関係は1:√2で、下のようなモデルにすることで二つの領域を結び付けて考えることができます。
これはオクターブの関係を1:2に分けたことでその中間が√2という値を持つ音になったからです。
この節(ふし)のような存在を利用し、次のようなモデルを作りました。
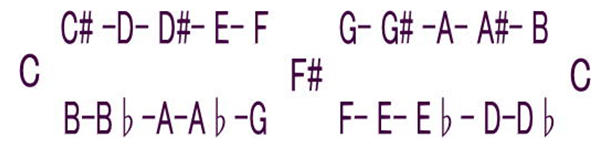
増四度環モデルです。
f#節を挟んで上方秩序と下方秩序の6音を上下で組み合わせることで12音全ての音種類が現れ、それが二つの鎖のようにつながれた音階モデルです。
この環において左半分の環を「表面環(明環)」とし右半分を「裏面環(暗環)」と呼ぶことにします。
ここで二次的な増四度も姿を現します。基音エリアのd#とaです。この音程関係も増四度なのですが、cとf#は音名も共通して上下に配置されるのに対して、d#とaはそれぞれが対面し、二次的な節を作っています。

ここで次のような表記を作っておきます。
Cu5=sCu5
F#u5=hCu5
D#u5=whCu5
Au5=wsCu5
sはSurface「表面」とし、hはHide「裏面」、wはWing「側面」とします。cを基音としたとき、仮想立体的な配置をイメージしてください。
これにあわせて十二音連関表にもc・f・gの縦の列を表面属、d#・aの縦の列を側面属、f#の縦の列を裏面属としました。
たとえば以下のようなテンションとしての付属音などとする発想です。
Cu5(d#)
これはcの上方五度領域の和音に側面領域基音を加えた和音です。また和音を合成することもできるでしょう。
Cu5(Au5)
この和音は、c,c#,e,g,aという集合です。
これを音階としてC△のコードの上でアドリブ音階として用いると「Cジャーコード上でCの側面領域の和音構成音をアドリブに用いた」という説明になるかもしれません。