2018.6.10⇨2020.10.17更新
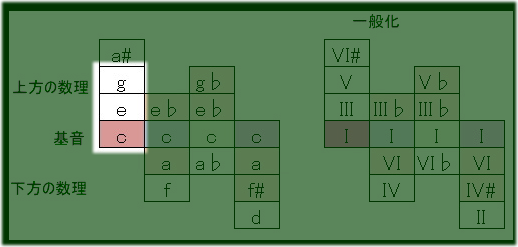
あとはこの表からどの音を使うかをその都度定めるだけです。
最初はいちいち考えますが12音を全て使えるので、あとは思考のクセ、パターンが音を自在に選んでくれます。慣れだけです。皆さんは皆さんの音選びの方法を考えてください。
機能和声は上記の開いたとこだけを用いて作られた音楽理論です。
上記はcという1音に反応するのはc,e,gという三音とします、ということです。そしてそれが機能和声論です。
一つの音から1度3度5度の音が親和すると決めてみましょう。
そうなると、C△ではどんな音集合が作れるでしょう。
c⇨c,e,g
e⇨e,g#,b
g⇨g,b,d
ですね。
つまりC△の上では、
c-d-e-g-g#-b
という音集合を作ることができます。
しかし調性音楽ではC△においてg#は使いません。基本となる音階の中にないからですね。
ある意味では機能和声的音楽もまた「使える範囲」を決めていたんですね。
みなさんは誰かが作った仕組みを学んでいるだけです。だから一方でどこまでを取り入れ、どこからを自分で考えるかあとで決めて自分の音楽を作っても良い、とも言えます。
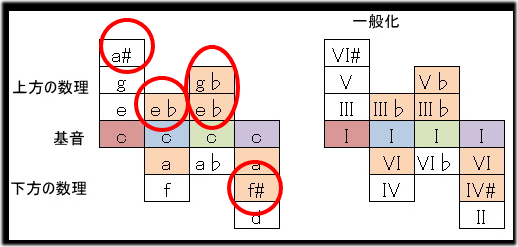
この反応領域を全体まで反応させると、赤丸で囲ったような音も出現します。いわゆるブルーノートです。
そしてc#とbだけが出てきません。これは私が決めたこと、というより、私が選んだ仕組みを組み合わせた時そうなった、だけです。
だからこの自分ルールで行くと、cの上でbとc#は親和しない、となります。
しかしcの他にもう1音gを入れたらどうなるでしょう。
cの親和音モデル全体
c-d-d#-e-f-f#-g-g#-a-a#
gの親和音モデル全体
g-a-a#-b-c-c#-d-d#-e-f
となって12音全て使えるようになります。
つまり、二つの音が同時に鳴っていたら、その時点で12音全てが使用可能になるわけです。
二和音鳴ったら12音は全て使える、という形ができあがります。これが欲しかったんです笑。ちょっと狂気にも思える感じかも、ですが。
みなさんがモデルを作るとき、基音の半音上下の音に親和を与えたいのであればそのようになるモデルを作れば良いと思います。
コードではコードスケールを使う、と言ってもあなたはコードスケール自体を使っているのではなく、手グセによるフレーズや、シークエンスを用いることが多いと思います。あなたもいつの間にかあなたのやり方を作っていると思います。
本当は個々人の音楽モデルが異なるからこそ違う音楽ができるのだと思います。