当ブログ音楽理論関連記事目次はこちら
ここでは下方倍音とその周辺の情報を扱います。
当ページは私個人が用いている下方倍音的存在の活用方法も含まれます。専門研究の方は文脈や内容にご注意ください。
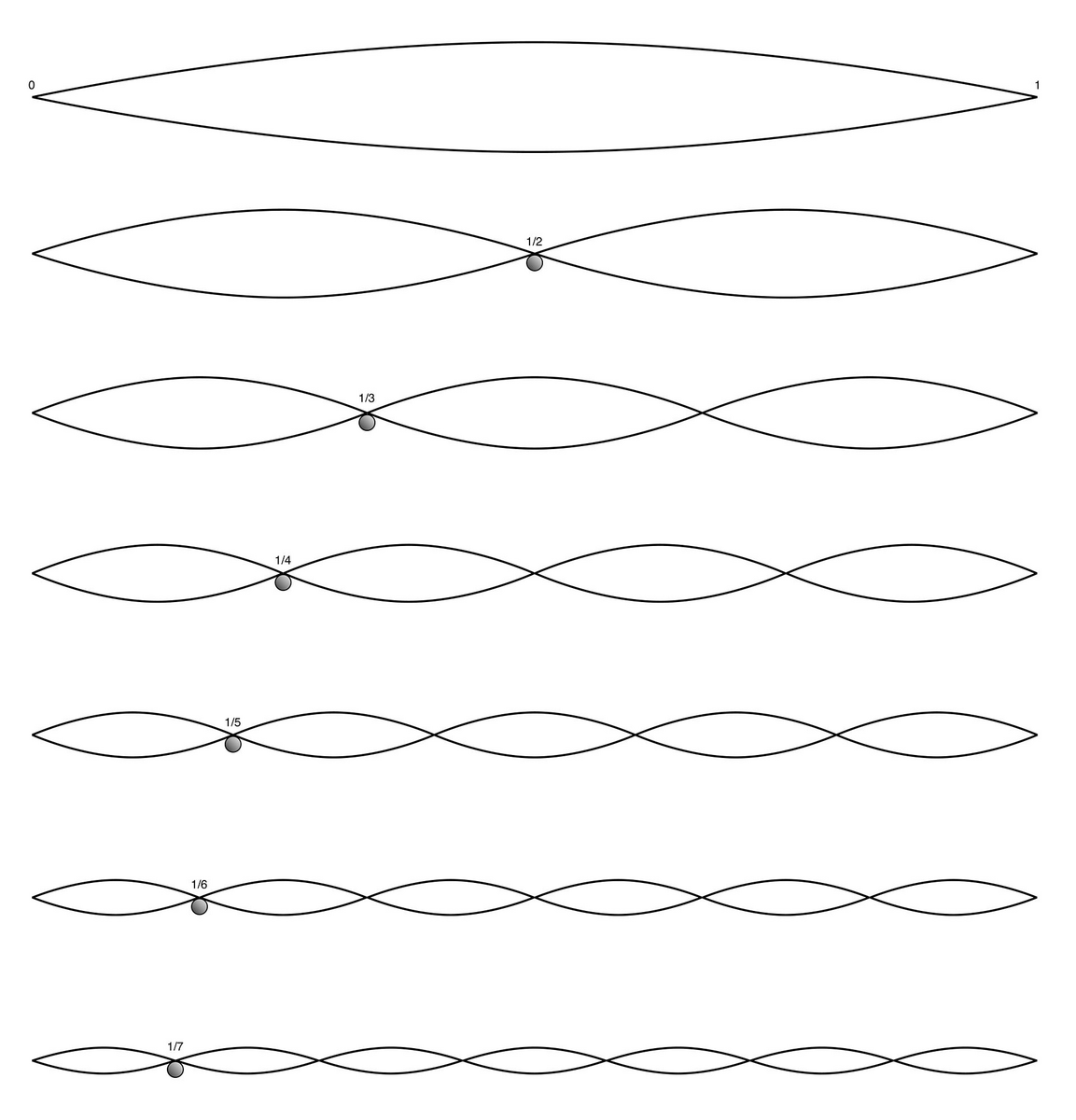
下方倍音は振動数を整数の逆数で割って生み出される計算上の概念です(短三和音がここから生まれたわけではありません。その類似性が後付けされただけです)。
c e g
という三音それぞれを基音とした時のそれぞれの下方三倍音は、
f a c =F△
てす。そして同様にそれぞれの下方五倍音は
a♭ c e♭ =A♭△
です。これらはC△をIとしたときのIVやVI♭です。これらの和音は皆様も楽曲で用いていると思います。下方倍音的存在は身近にあります。
上方倍音と下方倍音が計算上で生み出す世界を用いて再度音楽理論全体を見直してみると、各種音楽理論は刷新されると思います。
数理という概念を導入すると「聞こえない音」という考え方がそこにあることがわかります。下方倍音列も物理現象として極めて存在しにくいですが、その数理は美しいです。あとは個人の方法論が、そうした「数理の美」を用いるか用いないか、の選択です。
ここから展開して、今ならエモさと言われる儚さ、昔なら侘び寂びと言った魅力的な精神存在を私たちは理解できます。崩れ落ちゆく儚さも美しさと表現するために私は下方倍音の概念を方法論上で活用しています。
- 下方倍音の扱いや言説について
- ピタゴラステーブルを元にして
- スティックスリップ現象によるサブハーモニクス
- 脳が下方倍音的存在に親和性を感じるから現実味が存在する
- 不定調性論における倍音数理の基礎
- 平均律の振動数
下方倍音の扱いや言説について
「下方倍音列理論」という音楽の理論が明確に存在するわけではありません。
下方倍音という用語(学術的な用語でもないように思います)は、私のような専門外(正統な音楽研究範囲外??)の人間が面白がって扱う側面や過去の関連著作の偶然も重なり、いまだ専門的な論術や発表現場で扱うのはちょっとした違和感を与える可能性もあります。
ここに書かれている引用先表記のない内容は、私の独自論です(おそらく海外に存在する、よりメジャーな独自研究の引用先を探し当てられていないということかと思います-"独自論"はwikiなどの"独自研究"扱いよりもさらに下位の扱いをしてください)。
このブログや私の関連教材以外のところで、同一の出典不明の言説やアイディアを見た場合には出典がこのブログである場合があります。十分に各位で専門洋書などを慎重にご参照ください。私も先行研究を見つけたらすぐに掲載しています。
ピタゴラステーブルを元にして
ピタゴラス学派による"ピタゴラステーブル"を応用すると下方倍音列の概念が生まれます。

古代哲学者時代からその存在(?)は概念として知られていたようです。
哲学者イワンブリコス(ランブリコス)はピタゴラスの研究家でしたが、彼がその本に下方倍音列の元とも解釈できるアイデアを書き記しています。
この表を元にギリシャ語のラムダ(Λ)という文字に形にしたモデルを書きこんでいます。

下記はグラハム・J・ジャクソンがAdolf von Thimusがラムダモデルを倍音列の列の表に昇華した図を掲載しています。

https://www.scribd.com/document/619875286
出典はこちらの記事に最下段にあります。
こういう本でもピタゴラスの図が紹介されています。
スティックスリップ現象によるサブハーモニクス
ピアノを鳴らしても物理現象として根音より低い音は自然には鳴りません。(差音による低音、耳の構造の中で仮想的に構成される音(?)の認識が感じられる可能性はあり得ます。また特殊な低音発声や演奏技巧として「サブハーモニクス」等の手法もありますが、これは下方倍音"現象"ではありません。)
また100歩譲って、奇跡的に何らかの複合要因でいわゆるサブハーモニクスが偶然(部屋の反響、共鳴、前出音との振動の打ち消しによる差音などが発生し)鳴ったとしても可聴範囲にない音であれば聞こえません(20Hz周辺以下)。自然倍音は音色に影響しますが、下方倍音が鳴っても、西欧音楽耳には濁るだけで不快になるだけです。
その不快さを逆に詩的に「もの悲しさ」と感じることを了承できる人にとって下方倍音列は短調の根源になるのかもしれません。そこは個人の独自論で処理してください。
弦の原理的に、基音よりも低い音は鳴りようがないわけで(ピアノの高い弦で、その張力のままそれ以上低い音は鳴らせない、ギターの6弦より低い音は弦を緩めないと出ない)、100歩譲って楽器/環境/音色セッティングの要因で、たまたま基音よりも低い音が物理的には生み出されてしまう場合がないとは言えない、と考えるのが現状は限界ではないでしょうか。
(参考)
なお、演奏技巧における"低い音"については、上記で"anomalous low frequency vibration=ALF"異常な低周波振動、などと呼んでいます。木村まりさんの演奏技巧が著名のようです。
Subharmonic Partita, by Mari Kimura
先の"サブハーモニクス"については、上記アダム・ニーリーさんの動画にて音叉を紙に触れることで440Hzより低い200Hzの音を出しています。これは紙に触れる回数が、その距離感(紙と音叉の振動の接触)で実際の音叉の振動の半分ぐらいだったりするから、という説明です。下記の紙(青い線)に触れた音だけが鳴ってると考えてみてください。振動数は半分になるわけですから、音程もオクターブ下がります。

音叉自体の振動なのか、紙などにかかる振動の折り返しによる打ち消しなども含まれた結果なのか、手で触れるときの微妙な距離感がブレるからなのか、とにかくこれで原音より低い音が出せるわけです。
これ自体は下方倍音現象というよりも、演奏テクニックによる低音の生成です。こうした低音を下方倍音とは呼ばず、サブハーモニクス、と表現するのがポップなようです。
しかも、サブハーモニクスは弦の長さに応じ1/2、1/3倍音などがランダムに鳴る、と説明しています。
これはどこまで意図的にコントロールできるのでしょうか。上方倍音も意図的にコントロールなどはできませんが意味が違うように感じます。
専門的には「ヘルムホルツモーション」または「スティックスリップ」という現象らしく、弦の振動現象を利用した演奏法が発生原因である、としているわけです。
下記ページ中段にヘルムホルツモーションの解説があります。
弦の毛が滑ってひっかかることで振動数が減少し、結果低い振動数となり、低い音になって現れます。
脳が下方倍音的存在に親和性を感じるから現実味が存在する
またニーリーさんも述べていますが、脳は欠けた倍音を補う能力を持っています。
例えばシンセサイザーで自然倍音の2倍音以降c-g-c-c-e-gを弾くと、演奏していない低い基音cが耳の中=脳の中?では感じられます。EQでも出ていない音が耳に確かに聞こえます(差音?の可能性もある?=その場合、EQで確認できる場合もできない場合もあります。弱い差音の実音自体も耳の中で増幅されている可能性ありです)。特に倍音たっぷりなFMシンセ的な音に顕著です。それはスピーカーも鳴らしていない脳の中で作られた基音です。
WAVESはこの特許も持っていて、それをMAXXBASSなどのプラグインに応用した、ということです。下記は同プラグインマニュアルより。
However, the harmonics of the bass guitar are indeed coming from the speaker, and your ear interprets these harmonics and creates the “missing fundamental” inside your head. This is a well-known psychoacoustic phenomena. MaxxBass takes this phenomena to the maximum, and gives you control of it.
Using this principle,MaxxBass can extend the perceived frequency response of a speaker about two octaves below its physical limitation.しかし、ベースギターの倍音は確かにスピーカーから聞こえており、耳はこれらの倍音を解釈し、頭の中に「欠けている基本音」を作り出します。 これはよく知られた音響心理現象です。 MaxxBass はこの現象を最大限に活用し、コントロールできるようにします。
この原理を使用して、MaxxBass はスピーカーの知覚周波数応答を物理的限界より約 2 オクターブ下まで拡張できます。
なんでそんなことになるか、というと、そもそも人類の音楽文化自体が、脳の空気振動認識構造に適した形で進化してきたからです。どちらかというと楽器もDAWもシンセも脳内が倍音を上手に聴き分けることを活用して作られているので、脳(または必要な聴覚関連器官)は自動的に倍音を生成(補完的に?)し、楽器の音色を聞き分け、脳内で生み出される倍音を勝手に聞いてしまっている、ということです。
「豊かな倍音」みたいな言い方をしますが、そもそも耳は倍音構造でしか音を認識できません。
上記のような著名な著書にも、脳自体が倍音を感じ取る能力により現在の音楽(音色)文化が成り立っている、という方向に解説がなされています。
人の聴覚器官や脳が倍音を選別/聴取する機能に優れた組織だから、現在の音楽文化のような形態になった、というのが実際のようです。
だから、実際の世界には人間が聴取できる存在以外に、振動現象を構成している何らかの現象がある可能性も当然あります。
例えば、ある音を思い切り鳴らし、壁などで反響する音と正確に打ち消し合うことが出来れば、振動数は半減し、1オクターブ低い音が生まれる、なんて可能性の世界もありえます。
ヘンリー・カウエルの下方倍音に対する考えはこの空気共鳴による下方倍音の発生の可能性を指していると考えられます。ようは振動波を打ち消し合う環境があれば、基本振動数より低い音が生まれる、という考え方です。
<参考>
ヘンリー・カウエルの音楽理論と実践― 『新しい音楽の源泉』における新たな音響素材の探求―
実際に鳴っていない音存在も知覚できる人間の耳の性質は日常の音楽にも知らず知らずに使われているでしょう。ゆえに厳密には「下方倍音は鳴っていない」とか「下方倍音は存在しない」という言い分は「そうだろう、今のお前の中ではな...」という程度の話になります。なぜなら相手の頭の中で響いてしまう音、相手の視聴環境によって聞こえが変わる存在を全て考慮したらこういった一元的な見方で結論したところでなんの解決にもならないからです。
「存在しないかどうか」は限定的な条件を組み込んだ際に、「耳の外では存在しない」とか「無響室では存在しない」とかいうことができる程度です。
脳内が下方倍音列的存在をその場の音響現象に関係した何かの拍子に感じたり、仮想的に作り上げることがあったとしても、不思議ではありません。
何を持って「存在しない」と決めるかが曖昧、なのが現状です。
EQの上で反応しなければ存在しない、というのであれば、人間の耳の中で勝手に作られてしまう音についてはどのように排除すれば良いのでしょうか。
50代以上になると12000Hz以上の音が聞こえませんし低い音も聞こえづらくなります。そして若い人の意見も聞こえなくなります笑。
その振動数比が持つ数学的関係をどのように理解し、どのように現状の音楽(理論)に組み込むか、それぞれの表現者が考えるところに面白さがあるんです。この感じが下方倍音がアマチュア研究家向きな"夢のある"テーマとして落ち着いた所以かもしれません。
そこで拙論は、
「音自体が外界には存在していない」
としました。音高/音色として実感するあの知覚感覚は動物の耳と脳が作り出している創造物です。でもこうすると音楽論は非常にシンプルになります。
自然倍音は楽器の音色としても認識されています。
「ピアノの音」であるか否か自然振動数の含有量/比によって判断できます。
人にとって、倍音とは「音色の素」です。
少し変な例えですが、手拍子を1秒間に3回叩いたら「手拍子3回」と言う情報ですが、1秒間に440回叩けたら回数ではなく「全体のトーンの高低」でその情報を認識するのが脳の特色、と言えます。人が生存していくにあたり、「多い振動回数」を空気の振動の回数ではなく「音程をもつ一塊の現象」として情報認識するほうが素早く認識でき判断に有利だったためでしょう。
"今1秒間に空気が100回振動したからきっとこれは雷が鳴っているんだ..."というふうに人は感じないで、あのゴロゴロゴロという「音」として音色と一緒に、今何が起きているかを肌で感じ取り危険を即座に認知できるように進化したわけです。
音色による感情への訴えです。
だから本来雷も「音」ではありません。
宇宙人の中には音を色や空気の圧力、温度や風力、光や波長で感じ取る種族もいるかもしれません。
研究では、耳の中では原音よりも低い音が作られているとされます。これがベース音に安定を感じる人の感覚そのものである、と言えます。自然と基音を補ってしまう性質からバスという概念があるんですね。バスがあるから安定するのは、音楽の真理ではなく、人間の聴覚構造における真理であり、自然を人間主体で捉えようとする見方によっては傲慢な行為とも読み取れます。
不定調性論における倍音数理の基礎
拙論では、音現象で考える前に比率に見られる関連性を独自論に活用しました。
ピアノの低いほうのc(ドの音)を仮にc1としましょう。
c1よりオクターブ高い音をc2とします。
そしてこのc1を、基準となる音「基音」としましょう。
実際のホールで実際の生ピアノのc1をがーーーんと弾いた時に、空気中に伝搬する振動の波が人間の耳の中の鼓膜を同じ数だけ振動させます。様々な反響と一緒に高いキーンという音(振動)が感じ取れるはず(脳内で鳴ってしまう音も含め)です。これらの自然に混じってしまう振動数を、「自然倍音(上方倍音)」といいます。
c2=65とすると、これは鼓膜を1秒間に65回振動させる、とイメージしてください。人はそこにピッチ、音色を感じる(鼓膜から脳へ電気信号として送られ音程情報に変化させ、脳が認識できる「音」に変換して認識する)ことで「空気振動を理解した」とします。この振動数の単位がHz(ヘルツ)です。
c2は65Hzだ、とか言います。
では次にこの65を比「1」とします。
比2であれば、65×2=130Hzですね。オクターブ高いc3です。
では比10なら?65×10=650Hzです。「65のcの10倍音=c10」と理解しましょう。
普通の生ピアノでこのc2を弾くと、整数倍の振動数音が自然発生します(空気中の波の共鳴、とピアノの中での弦の共鳴パターン、部屋の音響によって別の空気振動が発生する)。
ギターの弦で一番低い音よりも低い音が鳴らないのはそれ以上弦を長くできない、そして弦が細すぎるからですね。
弦の長さを短くすればするほど高い音は出ます。振動の折り返しによってその弦の上でより短い振動節がどんどんできるため高い倍音は自然発生します。
音を低くしたければ、元の長さよりも長い弦が必要です。
だから下方倍音は自然には鳴らないわけです。
人が作った音を鳴らす仕組みにおいて基音より低い音がならないようにできています。だからシンセサイザーでなら下方倍音を生成し鳴らすことができます。
また、複数の音が鳴ると二つの音の振動数の差音が音程となり混じっていく場合もあります。
自然倍音列(上方倍音列)を順に書き出してみましょう。
c2=65とすると、
2倍音=130
3倍音=195
4倍音=260
5倍音=325
となります。これを順に列していくのが「倍音列」です。
===
平均律の振動数
2の12乗根を求めることで、数値が2倍になったらオクターブ高くなる12の階段を計算で作り出したのが平均律です。平均律は人体によくない、という人もいますが、たとえば平均寿命だけ見たら、平均律の歴史とともに寿命は伸びています。また純粋に純正律だけを使った音楽の方が稀です。教会音楽ひとつとっても、純正律である箇所とそうでない箇所があります。またゴスペル音楽が濁った調律で歌われてもそこに人間らしさが生まれ、より温かみのある音色になっていることも事実です。何かが他よりも優れている、という宣言は前時代的資本主義型主張であり、結局差別や排他主義を生み、不安を煽るだけです。
本来はそれぞれが未熟でも、互いの良いところを持って支え合い、それぞれの良いところを見つけ、活用する、活躍させる、という考え方でどんな場面でも排他的にならずギリギリまでクリエイティブになれるよう、外的要因に負けない精神性を築くことこそ重要です。
音名= 振動数
c4= 261.6256
c#/d♭4= 277.1828
d4= 293.6648
d#/e♭4= 311.1276
e4= 329.6276
f4= 349.2282
f#/g♭4= 369.9944
g4= 391.9954
g#/a♭4= 415.3047
a4= 440.0000
a#/b♭4= 466.1638
b4 = 493.8832
c5 = 523.2512
これによりオクターブ上のc5はc4を二倍した数になります。
261.6256×2=523.2512
平均律は発明であり、バッハの平均律クラヴィーアをはじめ、多くの優れた感性の持ち主が活用する調律です。
その2に続きます。
倍音についての参考記事