<下方倍音列って何?>
下方倍音列は、整数の逆数倍で現れる、と濱瀬元彦先生の著書『ブルーノートと調性』等でよりポップに紹介されて以来、日本ジャズ界の最深部(?)では知られています。
不定調性論もこれらのアイデアに基づいてその数理だけを利用していく、同書から生まれた方法論ではありますが、双方は異なる方法論(濱瀬理論に失礼なきよう)として頂ければ幸いです。この点についてはずっと以前に濱瀬瀬先生に東大講義以後、直にそしてメールでも釈明してご了解いただいております。
(同著を専門的に学習される方は、必ず濱瀬講師のスクールで直接指導を仰いでください。)
ブルーノートと調性 インプロヴィゼーションと作曲のための基礎理論(CD付)
下方倍音の計算方法は上方倍音の逆です。
c4=261.6256の1/2倍音は、
261.6256÷2=130.8128
となります。
1/3倍音は、87.20853...となります。どんどん音が低くなっていくのですから、いずれは1以下の振動数になり、無音=無振動に限りなく近づきます。
ここでは仮にC4=1としてみましょう。
1=C4、1/2=C3、1/3=F2、1/4=C2、1/5=Ab1、1/6=F1、1/7=D1、1/8=C1
この音集合が下方倍音列、です。
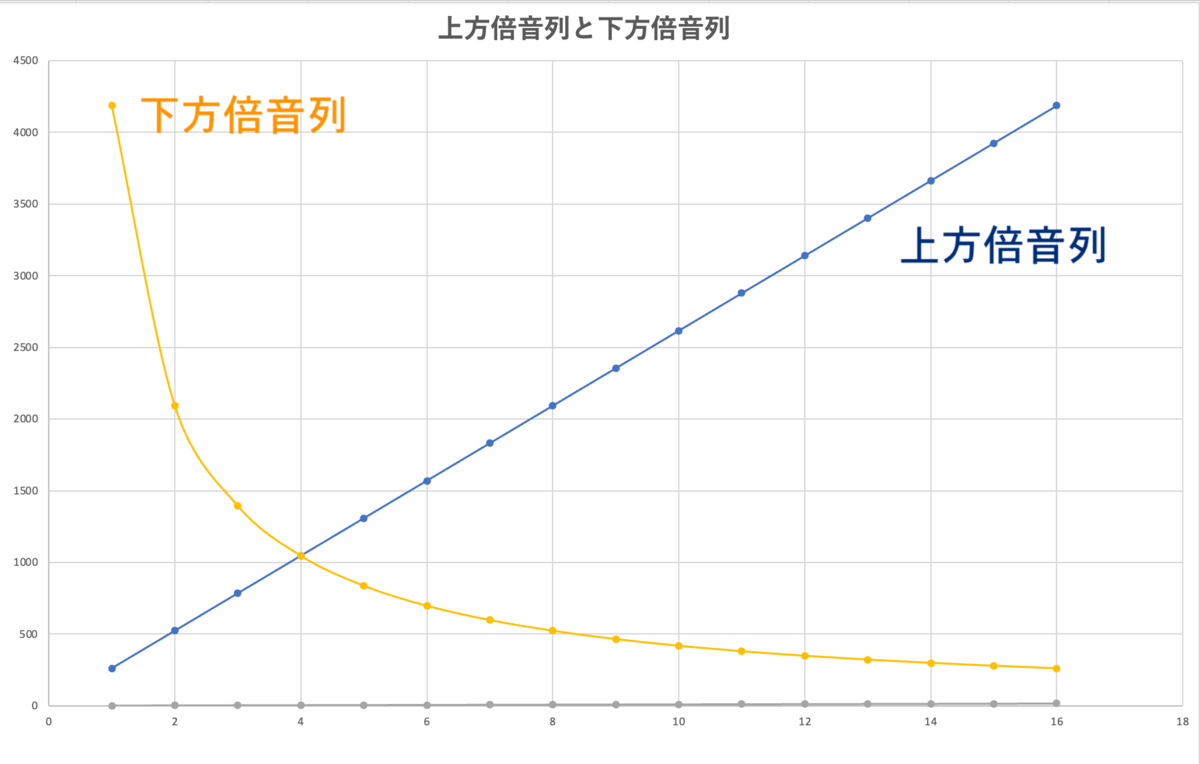
二つの関係は外観にも違いがあります。
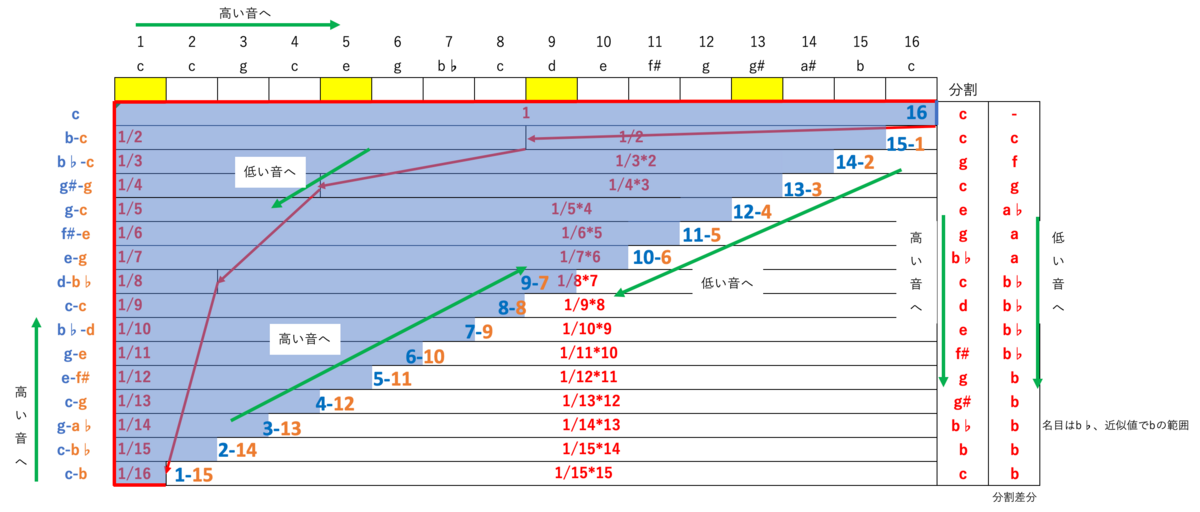
しかしその関係性は表裏一体のようです。
普段の音楽では、こうした関係性は無視されているでしょう。
しかし不可思議な音に美を感じる時、こうした関係性から、自分なりの美の根拠?を見つけ出し解釈することも可能です。その瞬間あなたの音楽に対する独自論が生まれます。そうした根拠発見の心理は、シミュラクラ現象とかパレイドリア現象などで説明したほうが良いかもしれません。
そう思うと見えてくるんです。私自身もそれかもしれません。
下方倍音列自体を直接方法論に組み込んで自分の作品に活かす(ことを愉しみにしている)人は、私を含めわずかでしょう。
しかし現状の音楽でも「サブドミナント」の位置付けが下方倍音の領域である、と言っても上手に説明できてしまいます。
サブドミナントという考え方が現在(ポピュラー方法論周辺)では主流なので「下方倍音」概念自体はいちいち用いる必要がなかったわけです。
逆に下方倍音を使っている、などと云うと、未だ迫害される恐れもありますので十分にご注意ください(そういう風潮を楽しんでる部分もあるんですが)。
そもそも、今使ったその音が下方倍音かどうか、なんて実際の音楽にはあまり関係ありません。
下方倍音は連続する仮想の音集合のことを指すので、実音になって使われたら、それは実音であり、倍音ではありません。上方も下方も関係なくなるんです。
下方倍音はいわゆる便利グッズの類です。
ポピュラージャズ音楽分析において下方倍音の数理があることで、ブルージーサウンドの意義や、現代的不協和音の美的感覚の根拠などの説明に使うとすごく便利です。
不定調性論も下方倍音の数理がないと大変説明が面倒になってしまいます。
問題は「協和」こそ正義と決めた西欧和声の価値観が根強く知識人の中に残っていることです。
人が自然の中で生き残るためには、不協和音を不協和で気味の悪いものだ、と認識できる必要があります。
雷の音を聞いて「あ、今からマラソンにでも行こうかな」などと思わないようにするためです。
不吉な音は不快でよくないものだ、と解釈できないと長生きできません。
しかし音楽は別です。小説の中で犯罪を犯すことが可能なように、音楽の中で不協和は甘美な存在になります。音楽を演奏することは手の込んだ妄想の具現化です。
同様に仮想の秩序である下方倍音は全くもって魅力的な存在になり得る、と言えます。
人体にとっての不協和音は、注意すべき存在であると認識しますが、音楽における不協和音は人体に危険はないため、短調の悲しさが本当に息苦しさをもたらすものではなく、むしろ美しさをもたらすように、人体に危害を与えない不協和音もまた時に儚さや震えるような美しさを醸し出す時がある、と人の感性が進化してきたわけです。麻薬みたいな感じ?
そうした意識の進化を歓迎するか、認めないか、で音楽へのアプローチも変わることでしょう。
不定調性論には、基音cに対して、12音は影のように割り当てられます。
これは今分からなくてもいいです。
c#=発生しない,もう一音必要
d=下方7倍音
d#=側裏面領域、またはfの上方7倍音
e=上方5倍音
f=下方3倍音
f#=裏面領域、またはg#の上方7倍音
g=上方3倍音
g#=下方5倍音
a=側表面領域、またはfの上方5倍音他
a#=上方7倍音
b=発生しない,もう一音必要
上下の倍音の数理がもつ対照性を用いて音連鎖を考えることで、不協和集合や伝統和声にない響きや連鎖が持つ別の美意識が感じられる、という点が下方倍音の集合概念を用いる意義です。
これらを用いることで音の関連性を容易に自由に生み出せる点が気に入っています。
要するに「その音は使えないって言われてるのに、ここでは使ったら気持ち良いけどなぜ?」という疑問にモヤモヤすることがなくなるんです。だって別の関係性が見えてきたら、それがそこで鳴って心地よい理由がいくつも頭の中に生み出せてしまうからです。それが妄想なのか、高度な数学なのか、はどうでもよく「さ、妄想ってないで続き作ろ」となれます。変に「avoidだから」「禁則なのに」みたいに感じることはなくなります。
同時に音楽理論自体にも興味がなくなるので(音の規則について-解釈次第でどうにでもなると知ってしまうから)、学生としてはあまり宜しくないかもですが。
具体的な自由度について、関係性の構築については、たくさんあるので一言ではまとめられないので下記に独自論の概念による12音の関係性の構築の意義と展開を一つ一つ書いてます。
ブルーノートや、不協和音、ノイズやアウトサイドプレイなどの存在意義やそこに感じるクオリアの意味を割り当てることもできるので私にとっては大変便利です。
これらの数理を用いて5音階の民族音楽と7音階の西欧音楽を紐解きます。
その3へ続きます。
